Categorical Perception of Colour

Click here and press the right key for the next slide (or swipe left)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (or add '?notes' to the url before the #)

Press m or double tap to slide thumbnails (menu)

Press ? at any time to show the keyboard shortcuts

What is categorical perception of colour?

Remember the idea that words like 'blue' pick out colour categories?

To claim that there is categorical perception is, very roughly and to a first approximation, to claim that perceptual processes are concerned not only with the particular colours of things but also with categories of colour like blue and red.

This is not a definition, only a very rough starting point.

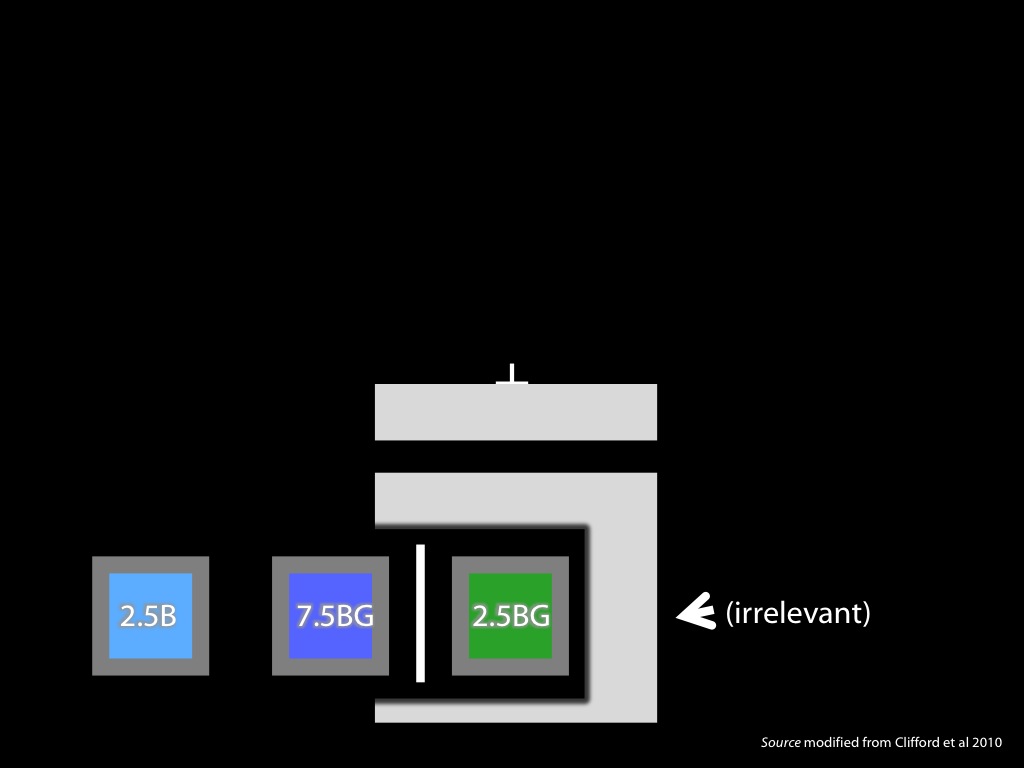
2.5B

7.5BG

2.5BG

Tell me what categorical perception is!

I can't tell you what categorical perception is. The operational definitions used in psychology are unrevealling. And the ways philosophers define it are wrong, or at least depend on unjustified assumptions.

But how can we study it without knowing what it is? We have to proceed by seeing what conclusions about it are supported by evidence. Then we can work back to infer what it is by asking what it could be if these conclusions are true. Put differently, we can start by asking, What is categorical perception commonly taken to explain?

At this point we should take nothing for granted and make no assumptions about what sense, if any, categorical perception involves either categories or perception. We are only asking, What is categorical perception commonly taken to explain?

‘categorical perception’

What is categorical perception of colour commonly taken to explain? The diagram below represents sequences of three colours. The vertical sequence shows three greens and the uppermost horizontal sequence shows a blue, a purple and a pink. div \begin{center} div \includegraphics[scale=0.3]{daoutis_2006_fig_A1.png} div \end{center} div \begin{center} \citealp{Daoutis:2006ij} figure A1 \end{center}

Each colour differs from its neighbours by the same amount according to a standard measure based on the human eye's abilities to discriminate wavelengths.

Yet the greens are often judged to look quite similar and the blue-pink-purple to look very different \citep[p.\ 12--7]{Roberson:1999rk}. When people are asked to name these colours, they often give the same name to the greens but different names to members of the blue-pink-purple sequence. And people are generally faster and more accurate in discriminating between members of the blue-pink-purple sequence than members of the green sequence (faster: \citealp{Bornstein:1984cb}; more accurate: \citealp[p.\ 22--7]{Roberson:1999rk}).

Let me show you how speed an accuracy of discimination are usually measured.

This is a 2-alternative forced-choice task (2AFC).

So far we've talked about three ways in which the blue-pink-purple sequence differs from the greens. The green sequence also differs from the blue-pink-purple sequence on other measures.

But these results are not confined to just two sequences. There is a way of dividing a colour space into categories that predicts all of these results and more. When the members of a sequence of colours fall into different categories, the colours are said to look very different, they are given different verbal labels, and the subject can discriminate them faster and more accurately than when they don't fall into different categories (all other things being equal). The fact that, for an individual subject, all these effects are predicted by a single way of dividing the colour space into categories is what categorical perception of colour is supposed to explain.

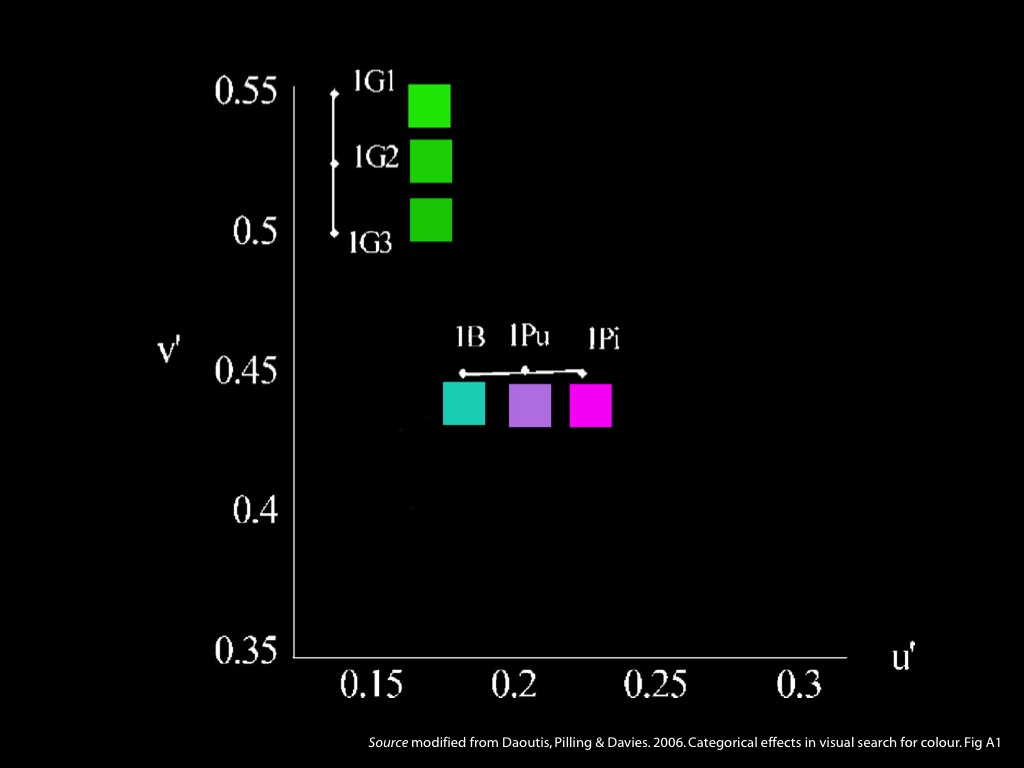
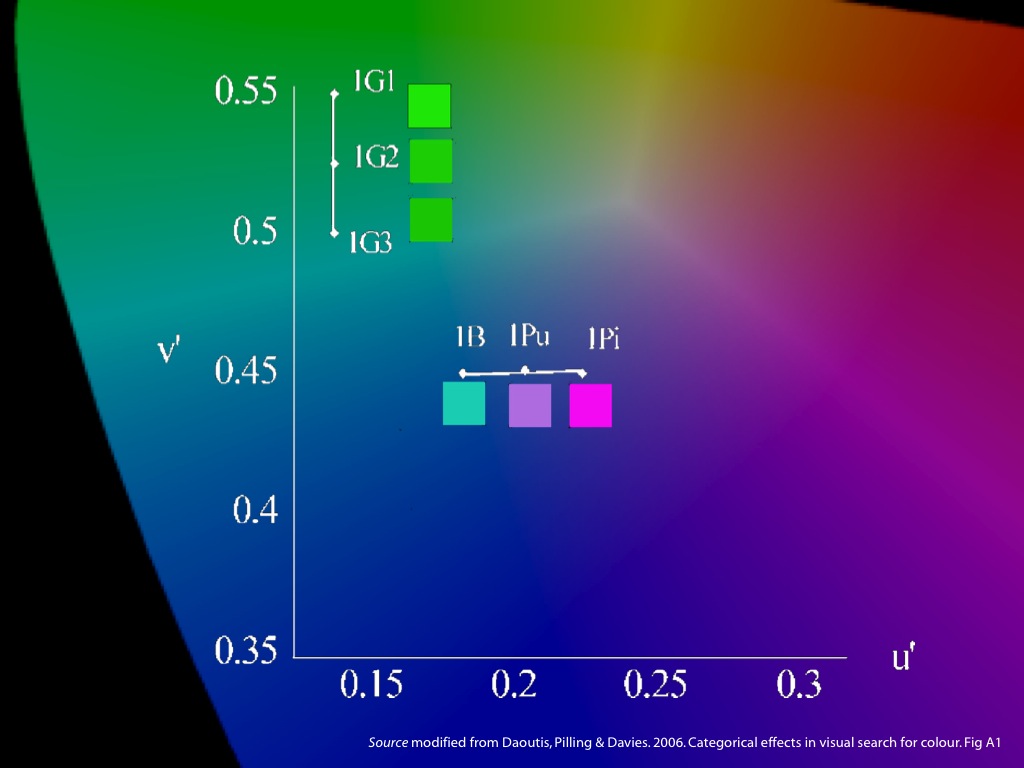
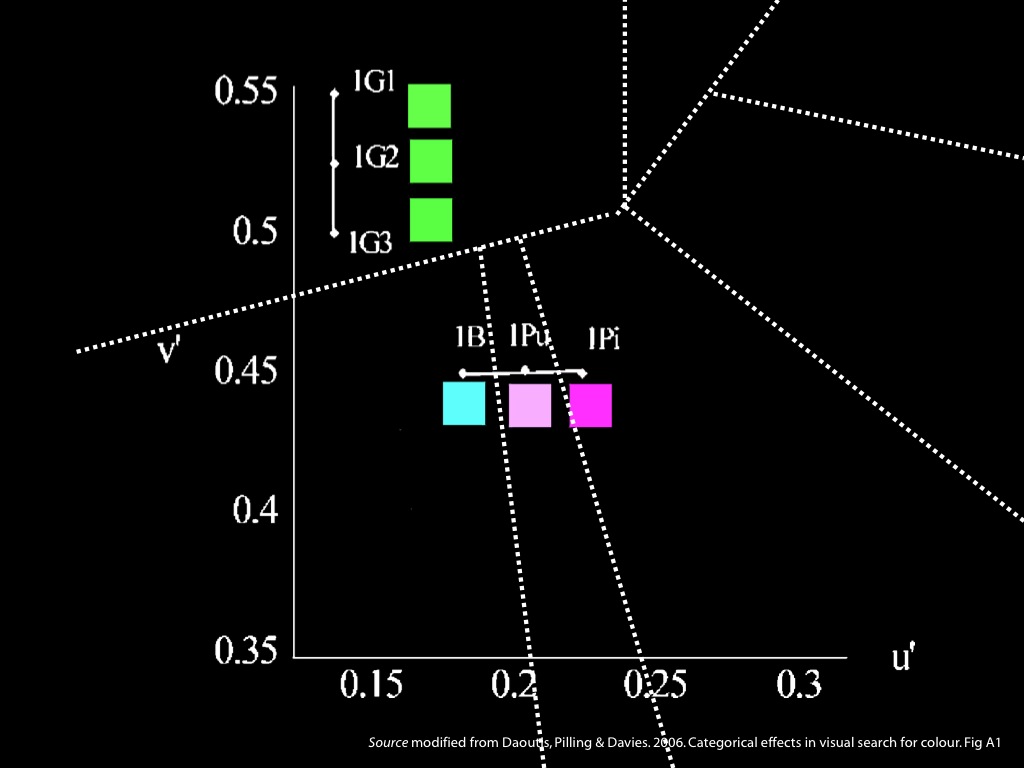
Reports of phenomenal similarity and difference
Linguistic labels
Speed and accuracy of discrimination

There are unexpected patterns in several phenomena including:

Reports of phenomenal similarity and difference
Linguistic labels
Speed and accuracy of discrimination
Pop-out effects
Change (odd-ball) detection

Now we're in a position to say what categorical perception is. A single way of dividing up the colour similarity space into a small finite number of equivalence classes enables us to predict a variety of effects including patterns in: reports of phenomenal similarity and difference, the use of linguistic labels, and speed and accuracy of discrimination.

This is a fact in need of explanation.

So what is categorical perception? Categorical perception is the process, whatever it is, that explains the unexpected effects. Now this way of defining categorical perception is not very informative. This is a virtue---categorical perception is something to be discovered, not defined. We might ask, what sort of process is categorical perception? In particular, we might wonder whether and in what sense it is a perceptual process. How can we discover more about categorical perception? One way to do this is to look for further unexpected patterns to be explained. It's just here that pop-out is useful.

Another measure on which the green sequence differs from the blue-pink-purple sequence is pop-out, which is defined operationally in terms of visual search tasks \citep[p.\ 117]{Treisman:1986pm}. First I need to explain what a visual search task is. In visual search tasks tasks, subjects are shown an array of objects and asked to identify the one with a certain property. For example, one might be shown an array of twenty animal pictures and asked to identify the cat. Normally the time it takes subjects to find a target increases linearly as the number of objects in the array increases. But when the target of a visual search is defined in terms of colour and the colours of the distractors are categorically different from the colour of the target, subjects can find the target just as quickly when it is in among 36 distractors as when there are only four distractors \citep[Experiment 1]{Daoutis:2006qk}. This is, the colours pop out.

\textbf{pop-out} ‘Such targets pop out of the display, so that the time it takes to find them is independent of the number of distractors’ \citep[p.\ 117]{Treisman:1986pm}.

When target and distractors differ in colour category there can be pop-out effects \citep{Daoutis:2006qk}.

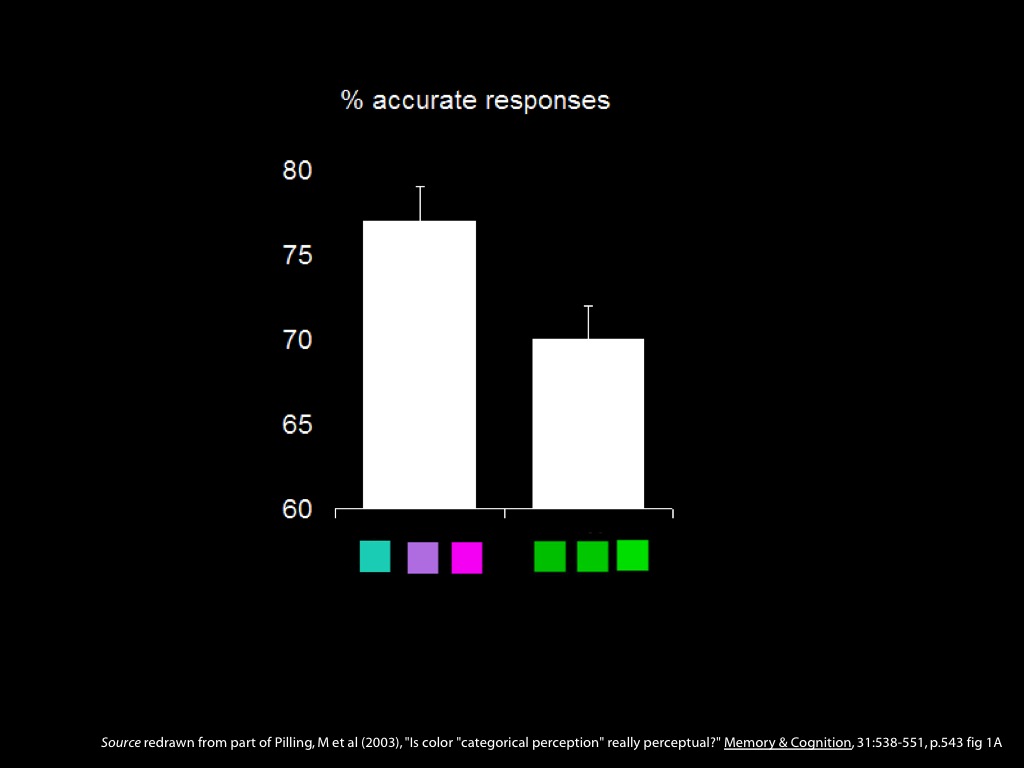
visual search task

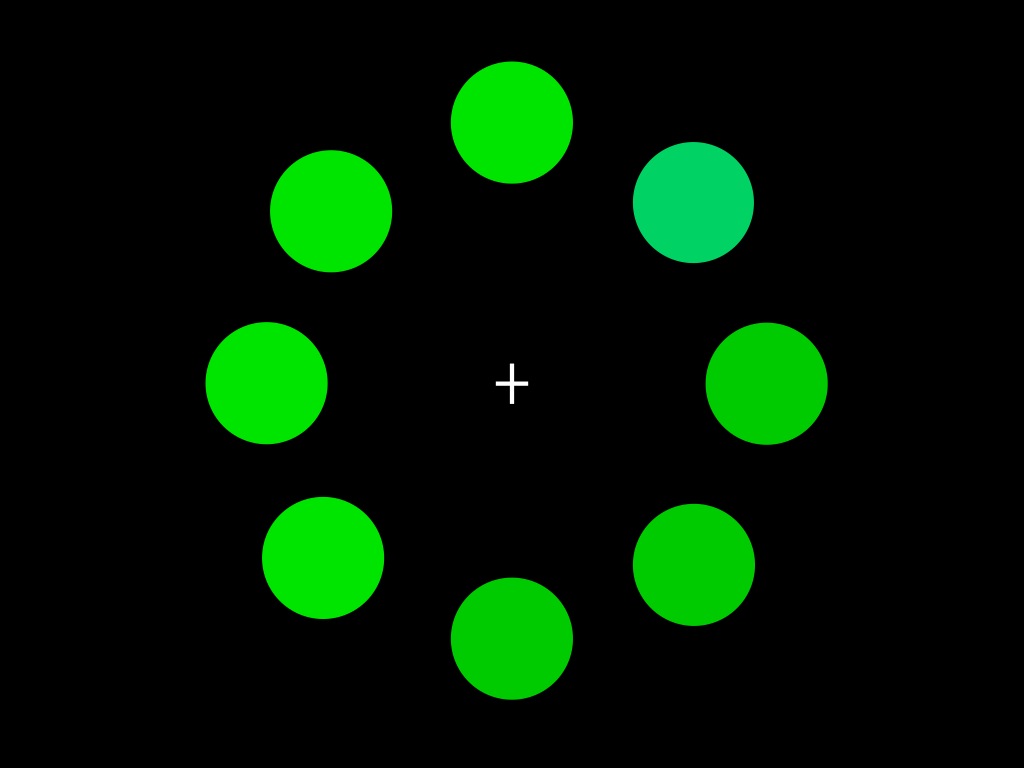
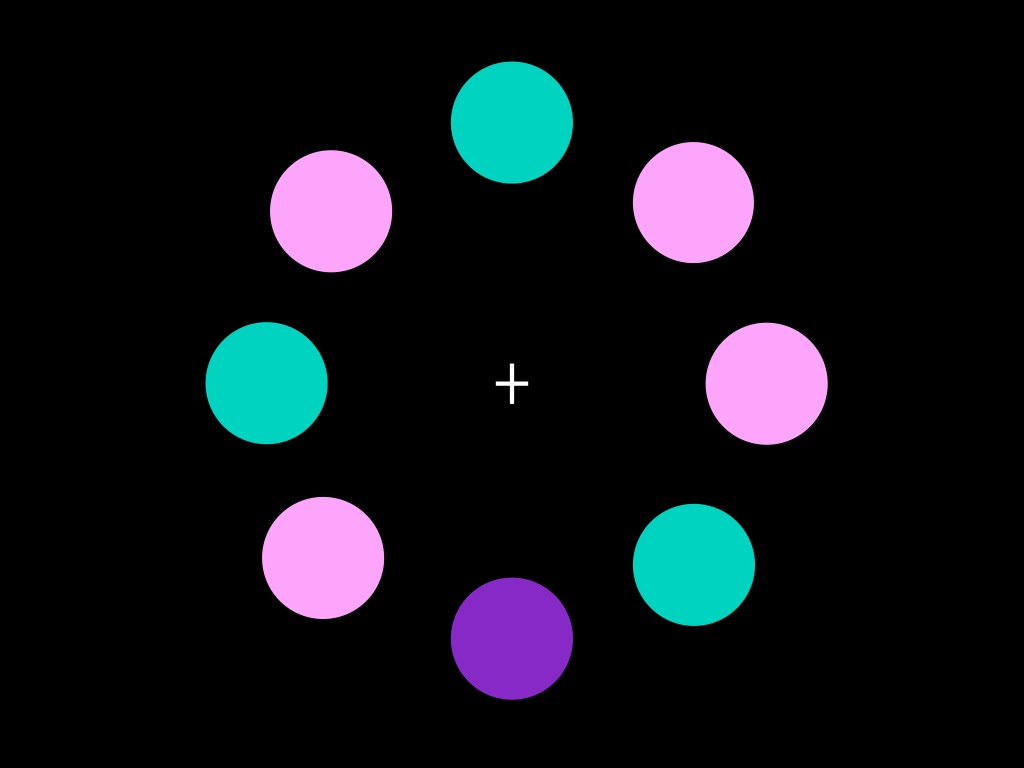
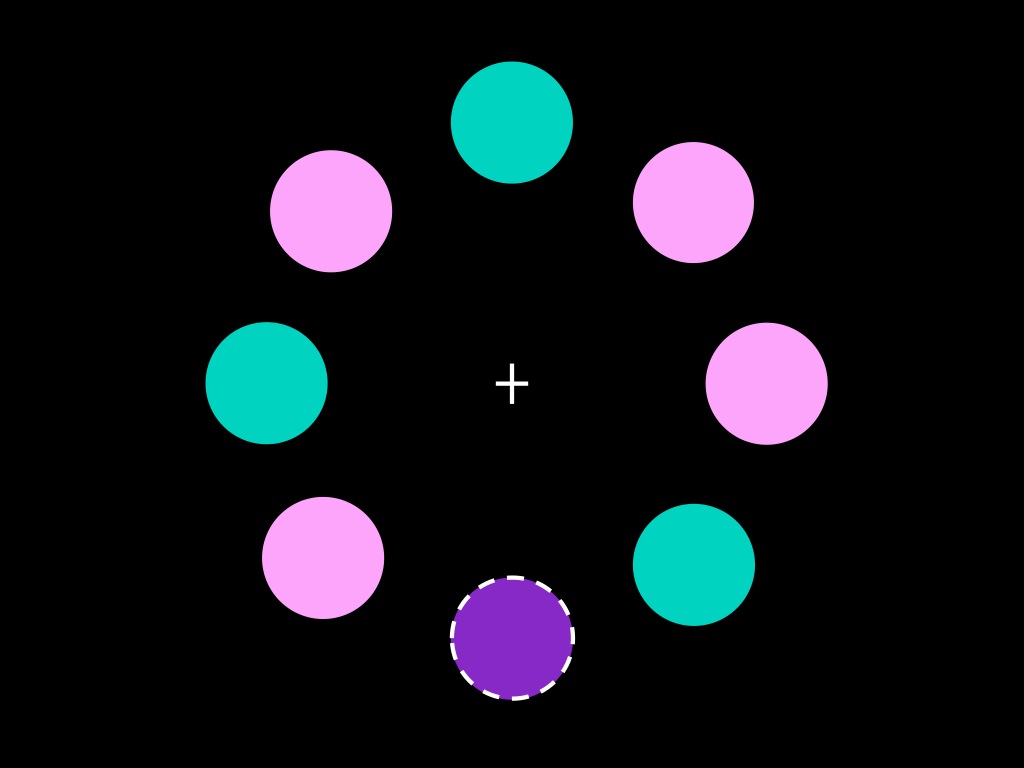
There are unexpected patterns in several phenomena including:

Reports of phenomenal similarity and difference
Linguistic labels
Speed and accuracy of discrimination
Pop-out effects
Change (odd-ball) detection

Recall that we defined categorical perception in terms of things it could explain. Now we can add pop-out to that list. This gives us more insight into what categorical perception is. In particular, it indicates that categorical perception is a perceptual process. And we can go on finding out more about categorical perception by finding out more about the things it explains. This is why I refused to define it at the start, and why you have to start without knowing what categorical perception is.

methodological aside

categorical perception vs core knowledge

Our topic is still categorical perception, but I want to pause here to reflect on how we've defined categorical perception. We should think of core knowledge using the same method. At the outset we don't know what core knowledge is. I just said it's like knowledge in some ways but not knowledge. We'll get a handle on it by looking at what it is commonly supposed to explain. More on this later; now back to categorical perception.

There are unexpected patterns in several phenomena including:

Reports of phenomenal similarity and difference
Linguistic labels
Speed and accuracy of discrimination
Pop-out effects
Change (odd-ball) detection

Among the things categorical perception is commonly taken to explain there are also automatic processes.

(This will be important later.)

A process is \emph{automatic} just if whether it happens is independent of the subject’s task and motivation (to a significant degree)

automatic process : whether it happens is independent of the subject’s task and motivation (to a significant degree)

For an example of a category effect which is automatic, I need to introduce you to the odd-ball paradigm.

In the odd-ball paradigm, you see a series of things that are all the same; and then, unpredictably, you see something different.

We can use sensitivity to odd-balls to measure the difference between the two blues and the blue-green pair.

This is useful because odd-ball effects can be detected very early in visual processessing, before attention kicks in.

They allow us to probe automatic processes.

odd ball

...

Now suppose we play you an odd ball sequence. We want to know whether an automatic process picks up on the difference. And we want to know whether the automatic process picks up on the difference always or only when a category change is involved. To do this we need to measure an event-related potential called vMMN (which is short for visual mismatch negativity).

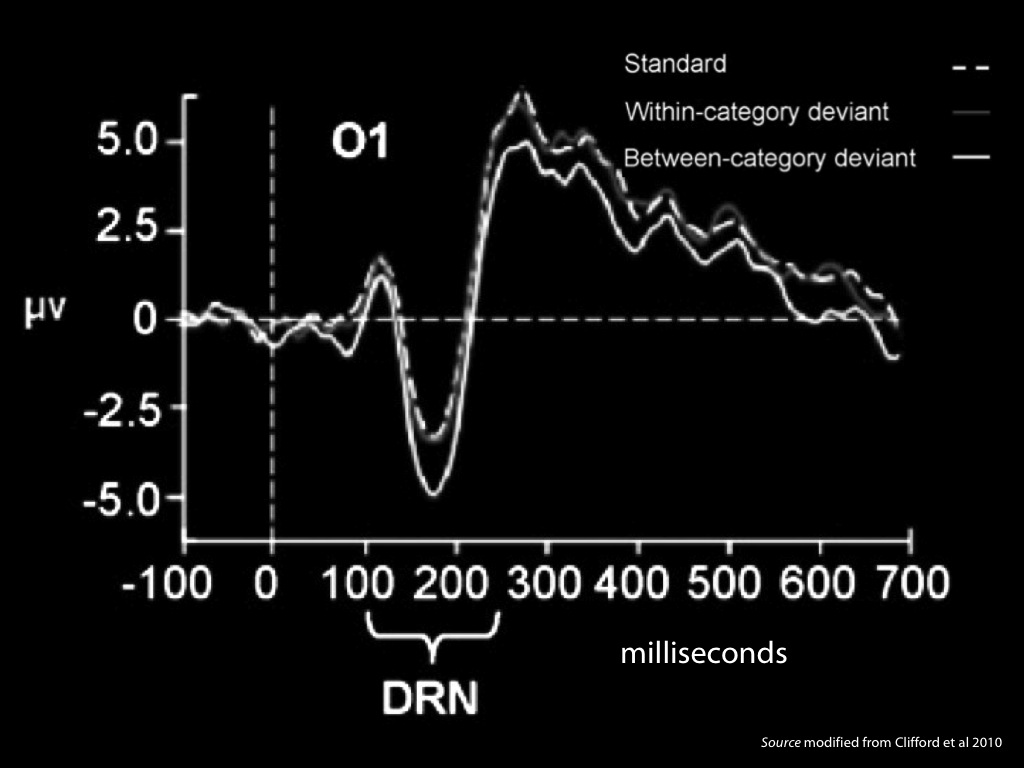
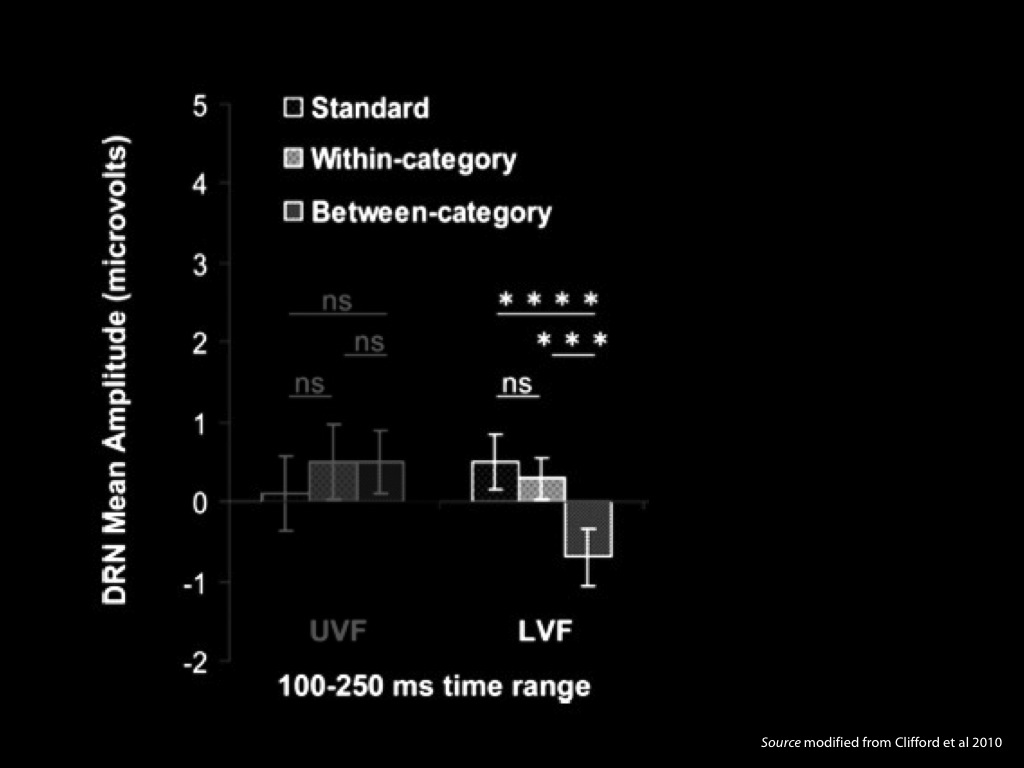
vMMN (visual mismatch negativity): an event-related potential thought to index pre-attentive change detection in the visual cortex

Now I need to explain what an event-related potential is.

An ERP like the vMMN stands to an overall EEG measurement a bit like the number 78 bus does to a collection of atoms.

While we're on methods, let's quickly talk about fMRI.

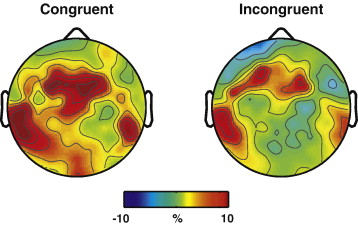
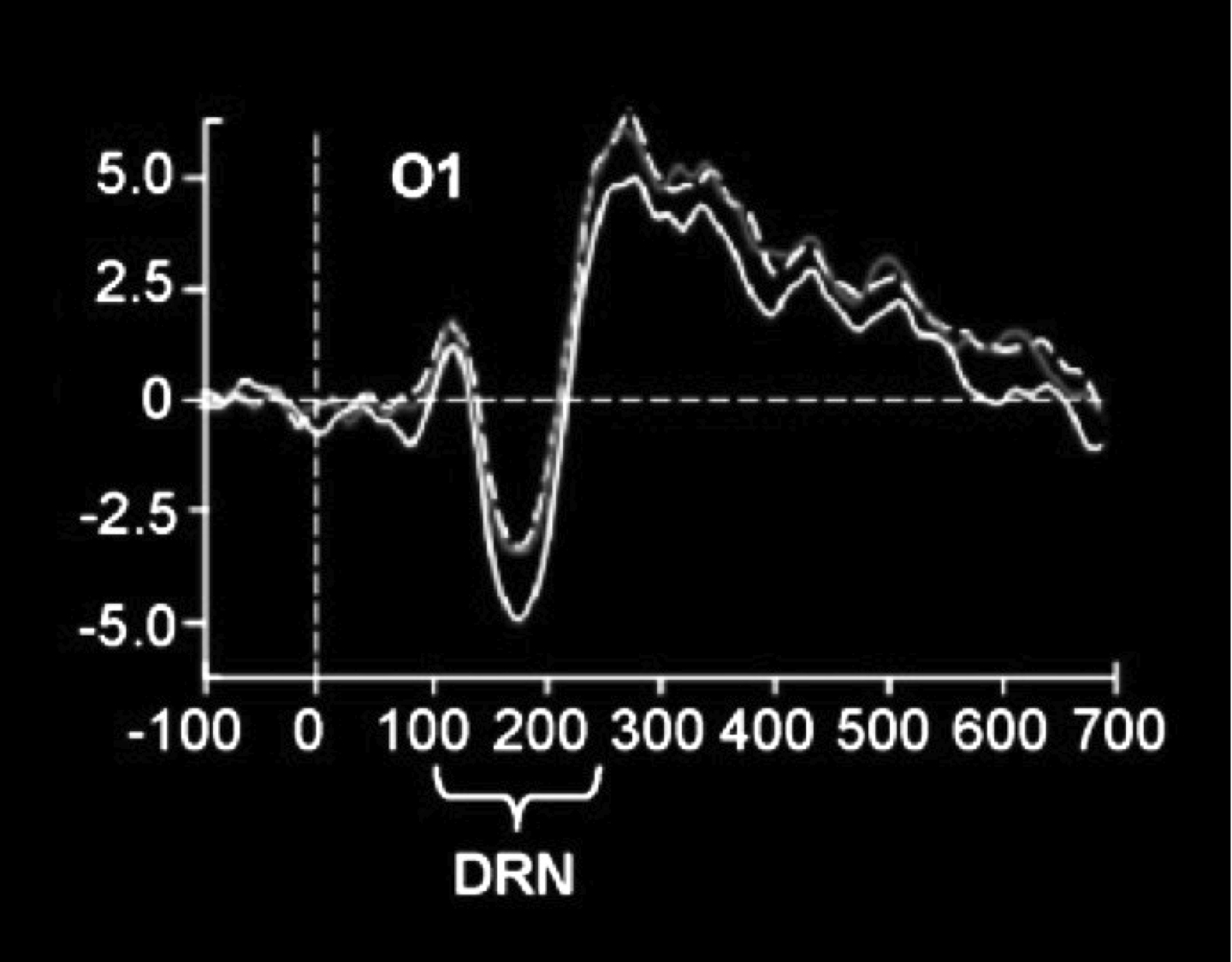
better spatial resolution
limited temporal resolution
subject can't move

So now we know what an event-related potential is, let's get back to the vMMN (visual mismatch negativity).

vMMN (visual mismatch negativity): an event-related potential thought to index pre-attentive change detection in the visual cortex

So let me show you a task that uses this odd-ball effect Fixate on this cross. And when you see the rectangle, press the space bar with both index fingers. That's it. Except that you also see a block of colour on every trial. You're instructed to ignore this block of colour. And generally that's easy because it's always the same colour. But just occasionally it's a different colour. In one condition, the usual and odd-ball colours are the blues. And in the other condition, the usual and odd-ball colours are cross-category, from blue-green. We're interested in whether there's a sign that your brain has detected the change when the odd ball colour occurs.

Put roughly, the results show that there is signal of pre-attentive change detection at around 100-200 milliseconds in the left visual field.

This is another way of presenting the same finding.

The vMMN is a DRN, but not all DRNs are vMMNs (see the paper).

Since this study \citep{clifford_color_2010}, \citet{he:2014_color} have challenged the results arguing that there is no vMMN when you control for irregularities in colour spaces using JNDs. However \citet{zhong:2015_shortterm} find a vMMN for newly trained categorical colour properties (which \citep{clifford:2012_neural}) didn’t. For our purposes, it isn’t essential that there is a vMMN. We should also be agnostic on whether categorical perception is pre-attentive. For us the important point is that it’s automatic. And all the studies agree on this.

There are unexpected patterns in several phenomena including:

Reports of phenomenal similarity and difference
Linguistic labels
Speed and accuracy of discrimination
Pop-out effects
Change (odd-ball) detection

A single set of categories enables us to predict all the patterns.

Hypothesis 1: There is a uniform explanation for all the patterns.

Hypothesis 2: The unexpected patterns all occur because a cognitive process categorises stimlui into these categories.

Hypothesis 3: This process is a broadly perceptual process.

Recall that we defined categorical perception in terms of things it could explain. Now we can add a further item to that list: odd-ball detection. Again, this gives us more insight into what categorical perception is. In particular, it indicates that categorical perception is an automatic process. It isn't only a matter of how you experience things to be.

Objection: theoretical confusion

1. In measuring categorical perception, you have to control for perceptual similarity.

2. This is done by using a(n approximation to a) perceptually uniform colour space.

3. A perceptually uniform colour space is one in which distances between shades correspond to discriminability. So equidistant shades are equally discriminable.

Therefore:

4. It is incoherent to suppose that differences in categorical colour properties could affect discimination when controlling for perceptual similarlity.

Can measure disciminability by different mechanisms.

[a] ‘cone–opponent dimensions of the second-stage mechanisms can be used as a perceptual reference’

[b] use discrimnation thresholds (JNDs) ‘the basic ability to detect small differences between colors. Sensitivity can be measured through discrimination thresholds’

[c] use ‘a speeded, suprathreshold discrimination task

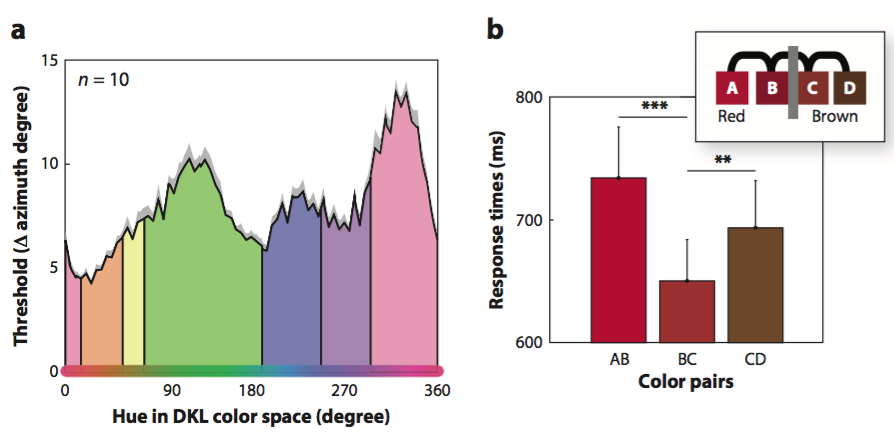
Witzel & Gegenfurtner 2018, figure 5

[caption:] ‘Category effects on color perception. (a) Categorical sensitivity. The diagram shows how the sensitivity to color differences changes across hue. The x-axis corresponds to hue in DKL color space, and the y-axis to discrimination thresholds. Adapted from Witzel & Gegenfurtner (2013). Note that the green-blue boundary is unlike the others in that it coincides with a local minimum of discrimination thresholds. (b) Categorical facilitation. The bars along the x-axis of the main graphic correspond to color pairs that are composed of the colors illustrated by the inset. The y-axis of the main graphic represents response times in speeded discrimination. Note that discriminating the color pair BC, in which B and C belong to different categories (i.e., red and brown), is fastest even though the distances between colors control for sensitivity to color differences. Adapted from Witzel & Gegenfurtner (2016). Abbreviation: DKL, Derrington-Krausfopf- Lennie. ∗∗p < 0.01; ∗∗∗p < 0.001.’

\citep[p.~488]{witzel:2018_colora}: ‘First, the known cone–opponent dimensions of the second-stage mechanisms can be used as a perceptual reference, and the sensitivity to color differences can serve as the category-probing measure. We refer to the sensitivity to color differences as the basic ability to detect small differences between colors. Sensitivity can be measured through discrimination thresholds under optimal conditions. In case categorical perception acts even at this basic level, sensitivity should be higher—and thresholds lower—at the category boundaries than within the categories. However, this is not the case (cf. Figure 5a): There is no category effect at this low sensory level of color processing (Bachy et al. 2012; Cropper et al. 2013; Danilova & Mollon 2014; Roberson et al. 2009; Witzel & Gegenfurtner 2013, 2018).’

\citep[p.~488]{witzel:2018_colora}: ‘Second, we can use those empirical discrimination thresholds as the perceptual reference and test for category effects on other performance measures (response times and error rates) in a speeded, suprathreshold discrimination task. In this case, category effects on response times and error rates have been observed around an isoluminant hue circle (Witzel & Gegenfurtner 2015) and at the red–brown boundary (Witzel & Gegenfurtner 2016) (see Figure 5b). We call these effects categorical facilitation in the sense that they facilitate speeded discrimination of suprathreshold stimuli beyond what is predicted by sensitivity. Interestingly, the categorical facilitation effects occurred only in na ̈ıve, unexperienced observers with high response times, but they disappeared for trained observers who became experts in the task and responded fast and automatically (Witzel & Gegenfurtner 2015).’

Objection: theoretical confusion

1. In measuring categorical perception, you have to control for perceptual similarity.

2. This is done by using a(n approximation to a) perceptually uniform colour space.

3. A perceptually uniform colour space is one in which distances between shades correspond to discriminability. So equidistant shades are equally discriminable.

Therefore:

4. It is incoherent to suppose that differences in categorical colour properties could affect discimination when controlling for perceptual similarlity.

So what is categorical perception?

There are unexpected patterns in several phenomena including:

Reports of phenomenal similarity and difference
Linguistic labels
Speed and accuracy of discrimination
Pop-out effects
Change (odd-ball) detection

A single set of categories enables us to predict all the patterns.

Hypothesis 1: There is a uniform explanation for all the patterns.

Hypothesis 2: The unexpected patterns all occur because a cognitive process categorises stimlui into these categories.

Hypothesis 3: This process is a broadly perceptual process.

This is actually made more probably by the Witzel & Gegenfurtner findings (doesn’t look like it could be to do with cone-opponent proceses, for example).

Keyboard Shortcuts?

Categorical Perception of Colour

Keyboard Shortcuts`?`